峰值電流式降壓型轉換器回授補償設計
Peak-Current Mode Buck Converter Compensation Design
摘要
峰值電流式降壓型轉換器 (Peak Current Mode Controlled Buck Converter)
是目前市面上相當普遍使用在消費型電子及電腦週邊電源管理的轉換器,本篇文章提供一套方式來設計峰值電流式降壓型轉換器回授補償,加上 Simplis 電路模擬工具、MathCAD
數學軟體定量設計與實際測量作驗証。
1. 峰值電流式降壓型轉換器之開廻路分析
峰值電流模式的組成,是由增加偵測外部電流轉換成電壓的電路 (Current Sensing Circuit),加至鋸齒波訊號 (sawtooth
wave) 所產生的迴路,將合成的訊號透過與誤差放大器的輸出比較來調整功率電晶體 [s] 導通的時間,其架構如圖一所示。
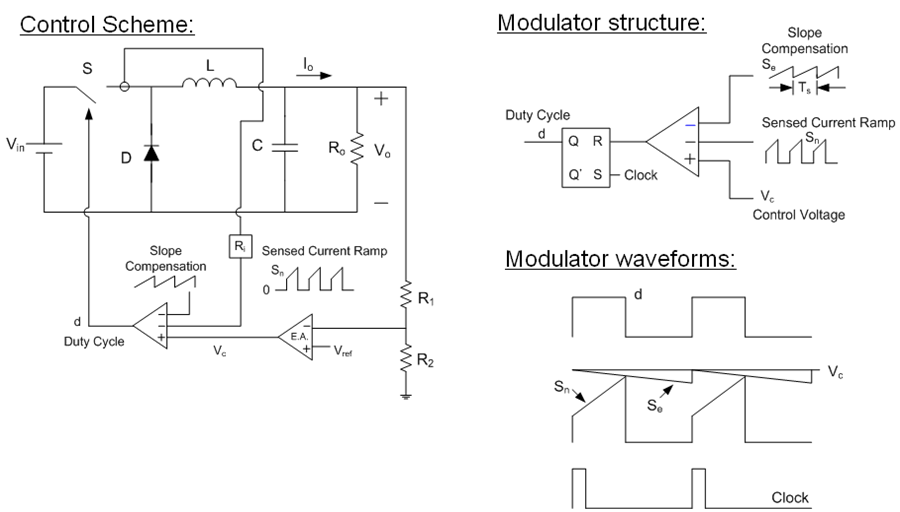
圖一、峰值電流式降壓型電路架構
電流模式當操作在責任週期 D > 0.5 時,會產生次諧波振盪 (Sub-harmonic Oscillation)。在 D < 0.5
的操作時,如圖二所示,其中TON 為每一週期 T 當中,晶體應該導通的時間,虛線為擾動訊號,實線為理想穩態波形,假設一開始有一擾動訊號,在
D < 0.5 的情況下,這表示即使有擾動訊號存在,在經過幾個週期以後,也會趨近於零,這也表示因擾動訊號產生的不穩定狀態會漸趨於穩定。在 D >
0.5 的操作時,如圖二所示,虛線為擾動訊號,實線為理想穩態波形,假設一開始有一擾動訊號,表示經過幾個週期後,其擾動訊號會持續被放大,使得系統不穩定。為解決上述
D > 0.5 之不穩定現象,在電路中須再加入斜率補償 (Slope Compensation),以改善系統不穩定知情況,其原理為加入一訊號為且與控制電路相同頻率的鋸齒波在電感電流的斜率上,使得責任週期在大於
0.5 的情況下,依然可以穩定操作。
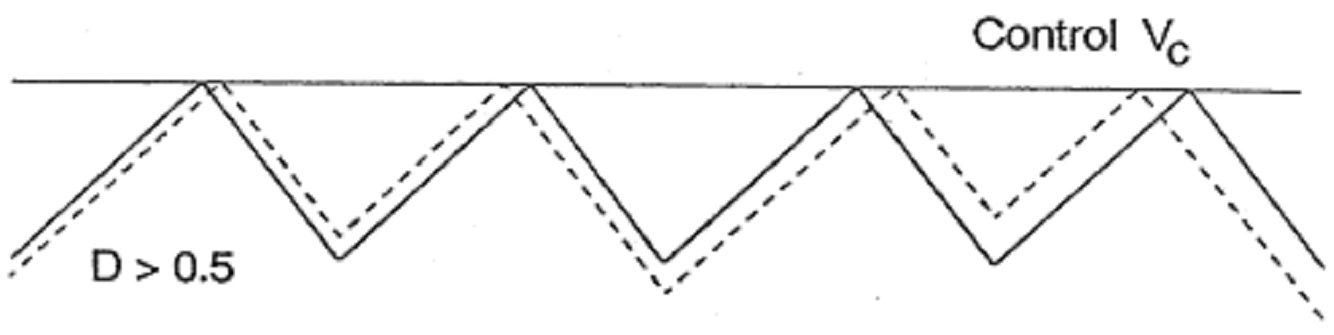
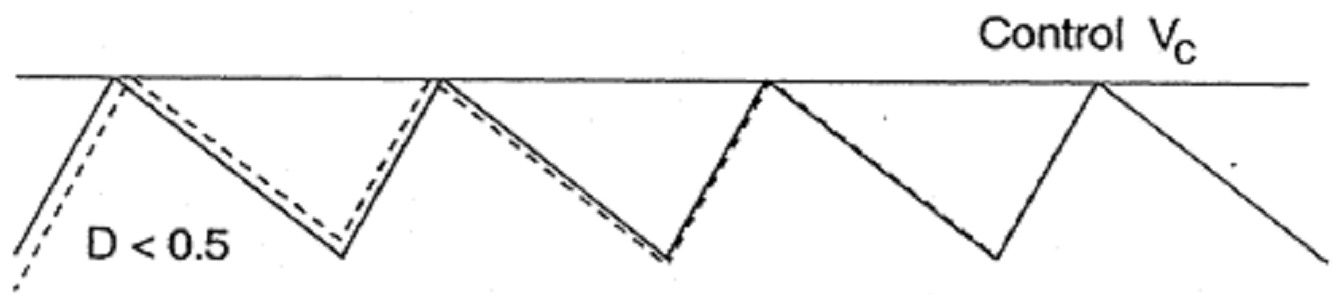
圖二、責任週期 D < 0.5 和 D > 0.5偵測外部電流 Ri 轉換成電壓波形
此段介紹峰值電流式降壓型轉換器的小訊號模型及參考文獻 [1][2],以 [1] 作者 V. Vorperian 提出的降壓型 PWM Switch
模型圖三與 [2] 作者 Raymond B. Ridley 提出的峰值電流式小訊號模型圖三導出的公式,加以應用在峰值電流式降壓型轉換器的補償設計。
圖三、降壓型 PWM switch 模型與峰值電流小訊號模型
以參考的文獻 [1] [2] 提供的式子,首先列出峰值電流式降壓型轉換器開迴路的轉移函數:
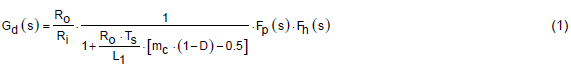
上式 (1) 的 Fp(s) 是表示開迴路時此架構主導低頻特性的式子 (2),由此式可得知有一個零點及一個極點。

上式 (2) 的是表示電偵測外部電流 Ri 轉換成電壓的電路對此架構所高頻處的影響,由此式 (3) 在高頻處會有兩個極點。

圖四顯示在低頻處有一個極點產生 (一個極點會以-20dB/decade 往下),而在高頻處有雙極點發生 (雙極點表示會以-40dB/decade)
往下,補充說明的零點是輸出側電容的 ESR 所產生。
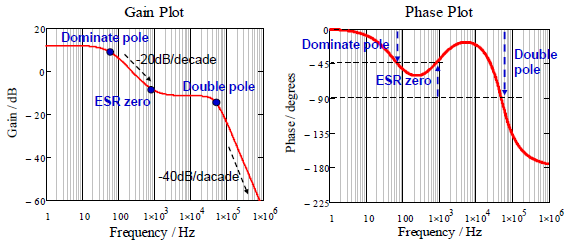
圖四、峰值電流式降壓型轉換器開廻路的波德圖
接下來是一步一步解析補償設計公式:
首先列出較精準的低頻極點公式:
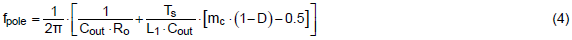
上述公式需要較高階的計算工具才能快速算出,所以想在較快時間內找出較為粗略的極點,提供以下式子供參考。

以下列出輸出電容所造成的零點公式:

以下公式是在二分之一切換頻率處有個雙極點的公式:

就以上述的公式,舉個例子呈現峰值電流式降壓型轉換器的重點特性。圖下為降壓型轉換器電路參數,輸入電壓是 12Vdc,輸出額定電流是 3A,輸出電壓是
3.3V,操作頻率是 340kHz,電感使用 10μH,輸出電容值是 44μF,輸出電容的 ESR 是 5mΩ。
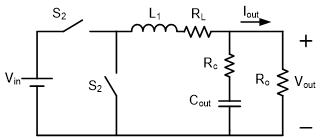
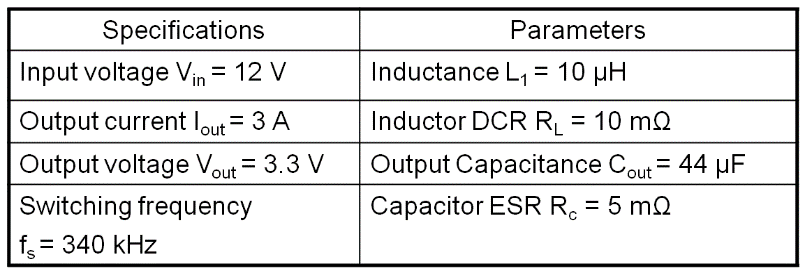
圖五、峰值電流式降壓型轉換器參數
代入上述參數到式 (4),求得較為精準的低頻一階極點落在 4.3kHz。
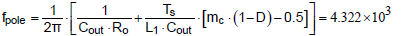
mc 為補償係數,定義為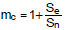 ,Se
為外加鋸齒波的斜率,Sn 為電流偵測波形在開關開啟時的斜率。
,Se
為外加鋸齒波的斜率,Sn 為電流偵測波形在開關開啟時的斜率。
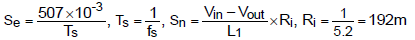 而較為快速的算法得到的一階極點落在3.3kHz。
而較為快速的算法得到的一階極點落在3.3kHz。
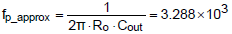
代入上述參數到式(6),求得較為精準的輸出電容造成的零點落在723kHz。
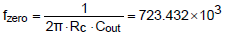
接下來是高頻率產生雙極點處,落在170 kHz。
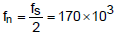
由上述代出的值,用 Mathcad 數學計算工具即可畫出以下的波德圖,下圖六顯示在低頻處 (3.28 kHz) 有個極點,而所使用的電容值的 ESR
較小,所以零點產生比雙極點還更高頻處 (723kHz)。
圖六、峰值電流式降壓型轉換器開廻路的波德圖範例
2. 峰值電流式降壓型之補償設計
上一章節介紹了峰值電流式降壓型的特性,接下來就來思考要如何補償才能使峰值電流式降壓型的系統穩定,由下圖七紅色線表示開廻路的增益曲線,在低頻處只有低的直流增益,過了在增益
0dB 時,是以 -40度/decade 的斜率往下,而低頻處的低直流增益會造成穩態誤差如圖九; -40度/decade 的斜率往下則會讓相位以 -90
度翻轉,容易有相位餘度不足的現象如圖八,造成系統不穩定。然而藍色線是設計閉廻路的增益曲線最佳化。其跟開廻路比較有以下的優點,低頻處有高的直流增益,可以減少穩態誤差如圖九;過了在增益
0dB 時,是以 -20度/decade 的斜率往下,可以讓相位以 -45 度翻轉如圖八,改善相位餘度 P.M. (phase margin) 不足的現象。
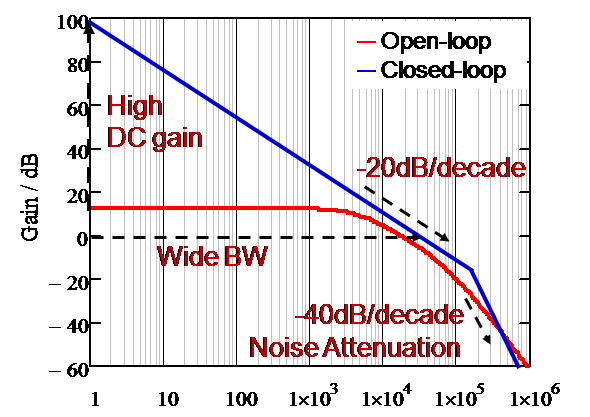
圖七、開廻路與閉廻路的波德圖比較
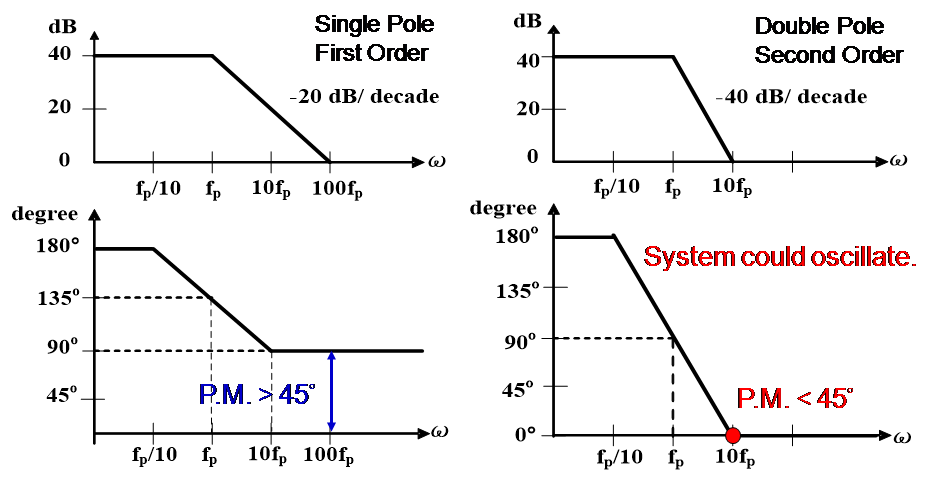
圖八、單極點與雙極點
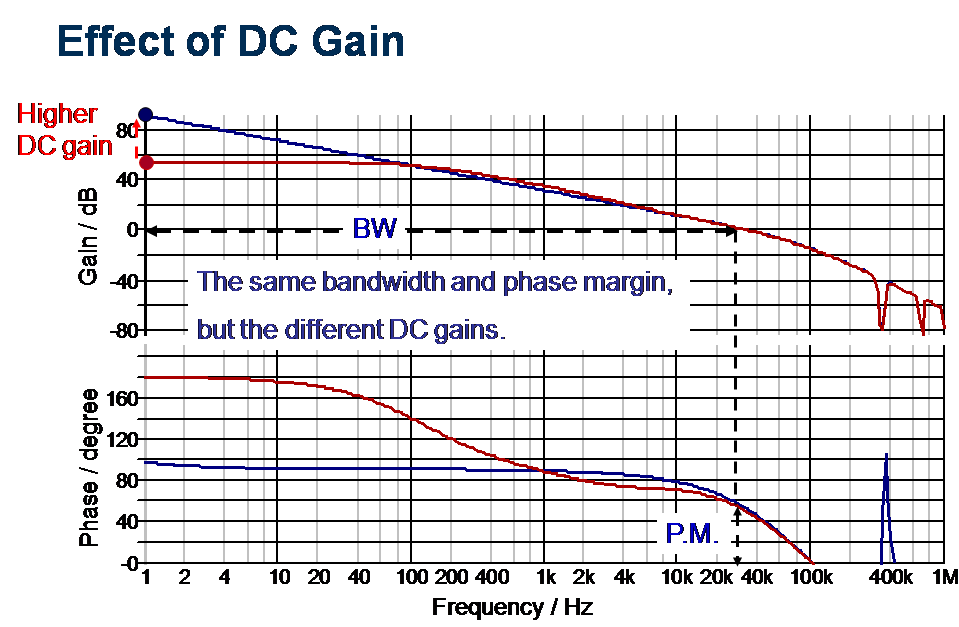
圖九、直流增益的影響
如圖十表示在高直流增益時,會得到較好的負載變化率,反之則會得到較差的負載變化率。
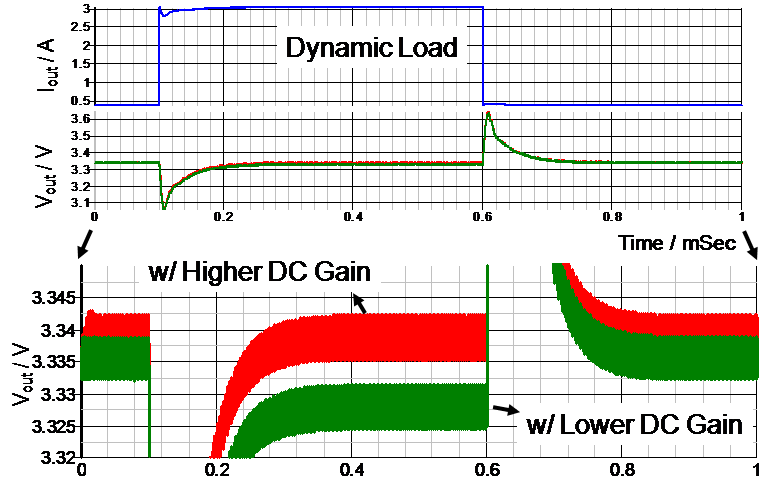
圖十、直流增益的高低對負載變化率的影響
分析上述不同參數對系統的影響,得知需要補償器來設計一零點來相消峰值電流式降壓型在低頻處所產生的極點如圖十一,讓交越頻率處是以 -20dB/decade
的斜率往下降,藉以得到較高的相位餘度,而在高頻率處利用補償器設計一極點濾除高頻雜訊。
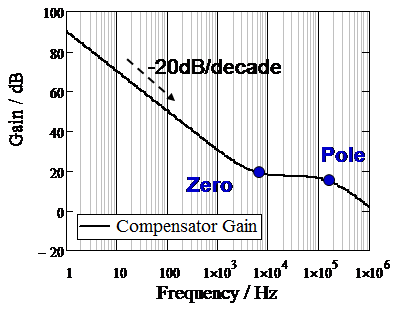
圖十一、補償器提供一零點與極點
如下圖以 GM-Type 為例子,因為 GM-Type 能提供一個零點與兩個極點,符合峰值電流式降壓型所需要之補償器。其中低頻的第一個極點由 Rgm
和 Ccomp 求得,第二個極點由 Rcomp 和 Cgm 求得,零點由 Rcomp
和 Ccomp 求得。
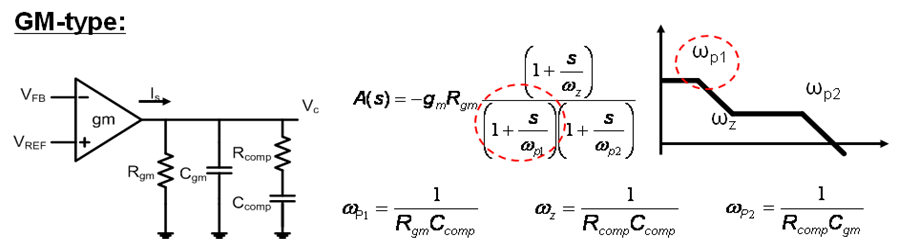
圖十二、GM-Type
接下來就正式進入補償器的設計步驟:第一步:設定交越頻率 (即頻寬),以此範例,操作頻率 = 340kHz,頻寬是設定在十分之一的操作頻率為準則。

第二步:補償器設計一零點去相消峰值電流式降壓型架構的極點。

第三步:補償器設計一極點在輸出電容的 ESR 造成的零點處或者 1/2 操作頻率,看此兩個條件,哪一個比較低頻,就優先選擇之,在此範例中 1/2
操作頻率比輸出電容的 ESR 產生的零件還要低頻,所以選擇 1/2 操作頻率。

第四步:將此式建入Mathcad 數學運算軟體,即能求得相位餘度為48度,在此作個補充,通常相位餘度設計大於45度為佳。
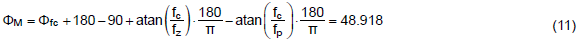
第五步:此式表示補償器在交越頻率處提升的直流增益為17.4dB。
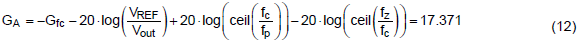
計算補償器的參數,在此例子得到Rcomp = 5.9kΩ,Ccomp
= 6.23nF,Cgm = 158pF。
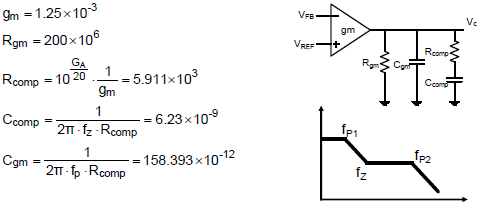
第七步:將上述值代入式 (13),鍵入MathCad 數學計算工具得圖十三,即為補償器的波德圖。

圖十三、補償器的波德圖
3. 峰值電流式降壓型轉換器之閉迴路分析
此章節加上使用 Simplis 模擬工具來模擬峰值電流式降壓型轉換器之閉迴路的頻率響應分析如圖十四所示。此電流式降壓型轉換器之閉迴路包括電流偵測電路、補償電路、斜率補償電路。
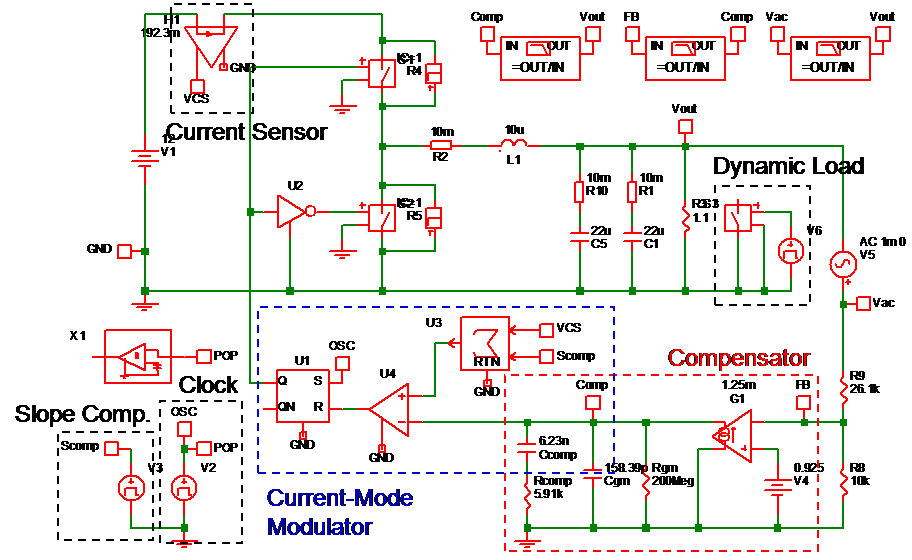
圖十四、SIMPLIS 模擬工具 (峰值電流式降壓型轉換器之閉迴路)
如圖十五所示,藉由上個章節所列的式子鍵入Matchcad 數學計算軟體(如圖中紅色線),加上使用圖十四 Simplis 工具 (如圖十五藍色點)
相互驗證,得知不論是用數學定量分析或用模擬工具,頻寬都為 34kHz,相位餘度都為 48.9 度。其結果都具一致性。
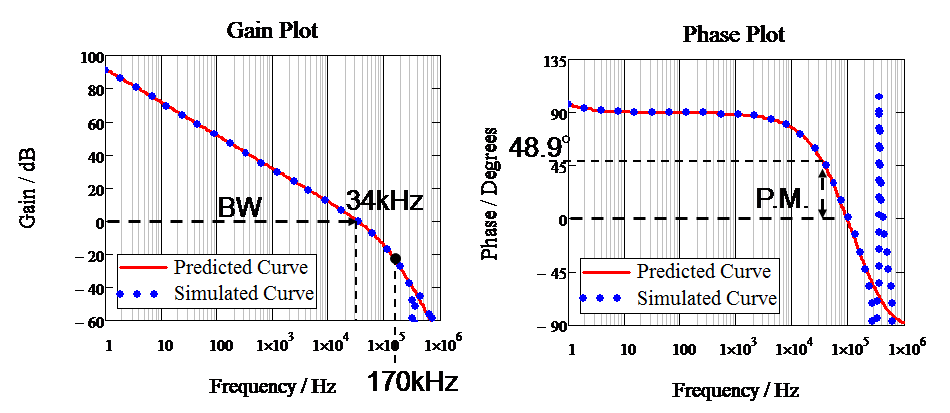
圖十五、mathcad 數學定量分析與 Simplis 模擬
圖十六所示,可以得知經過了補償器設計後,產生了哪些優點,第一、補償器(如黑色線)能在低頻處提高直流增益,紅色線為開廻路加上黑色虛線等於藍色線閉迴路。第二、補償器增加了頻寬,就如下圖十六藍色線的交越頻率較紅色線的交越頻率為寬。第三、補償器在高頻處加了極點,增加高頻雜訊免抑力(如高頻處藍色線較紅色線低)。第四、補償器設計的零點以維持足夠的相位餘度。
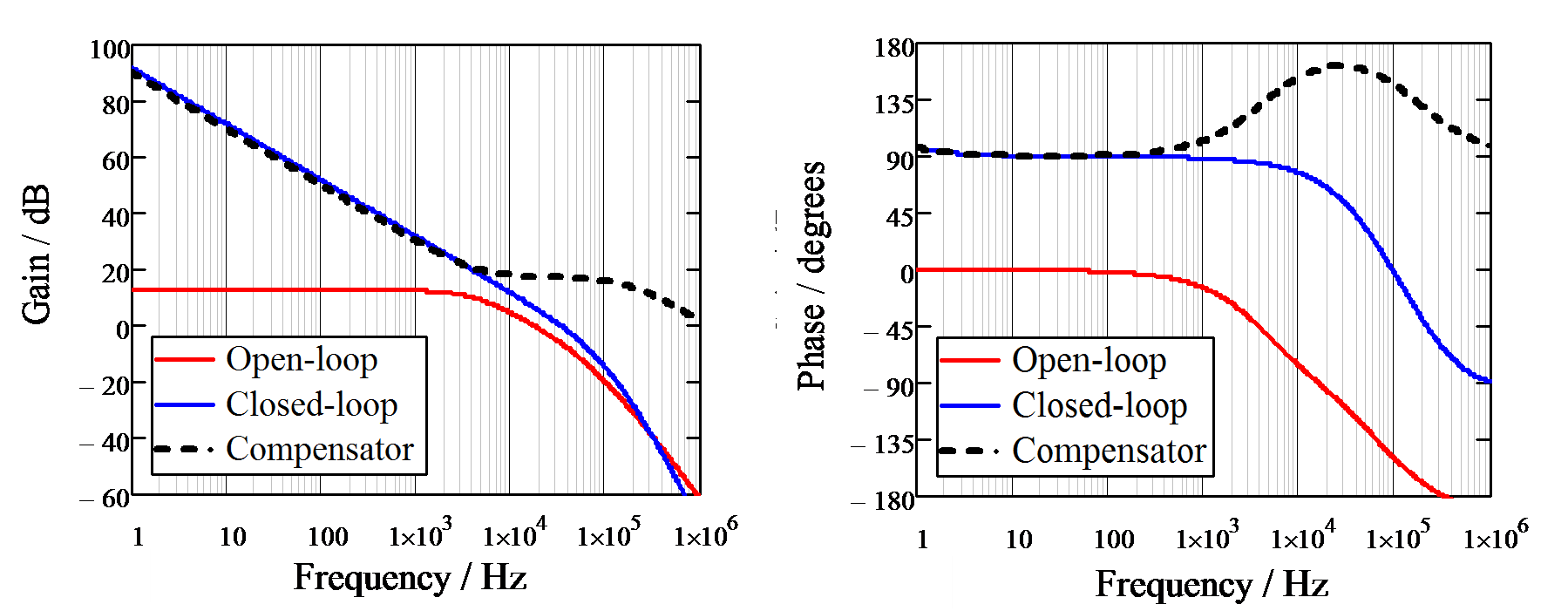
圖十六、開廻路與閉迴路之比較
如圖十七是實際量測圖,另外提供一擾動訊號,量測R點與A點的比較得知增益與相位,如圖十七右圖得知實作驗証(緑色線)定量分析(紅色線)是準確的。

圖十七、實作驗証閉廻路頻率響應
4. 結論
- 峰值電流式降壓型轉換器之開廻路在低頻處是一個單極點的系統,其原因是電路上加上電流訊號在系統上導致的。
- 其補償器容易設計,且能提供與系統相反極零點進行相消,使系統穩定。
- 提供之設計法則就是設法以 -20dB/decade 的斜率經過交越頻率,使其能達到足夠的相位餘度。